Gleichungen fünften Grades

Warum einige auflösbar sind, die meisten aber nicht

1824 beweis der norwegische Mathematiker Niels Henrik Abel, dass es für die allgemeine Gleichung fünften Grades keine Auflösungsformel geben kann. Das heißt, zur Berechnung der Lösungen von Gleichungen fünften Grades gibt es keine allgemein gültige Formel, die nur die vier Grundrechenarten und Wurzelausdrücke verwendet, um so die Lösungen aus den Koeffizienten der Gleichung zu berechnen. Gleichungen fünften Grades sind damit in prinzipieller Hinsicht "schwieriger" als Gleichungen bis zum vierten Grad, für die solche Lösungsformeln wie die Cardanische Formel für kubische Gleichungen bekanntlich existieren.

Allerdings gibt es durchaus spezielle Gleichungen fünften Grades, für deren Lösungen Wurzelausdrücke gefunden werden können. Beispielsweise ist

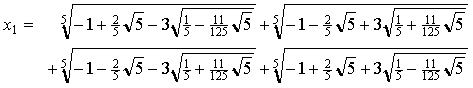
Lösung einer Gleichung fünften Grades

eine der insgesamt fünf Lösungen der Gleichung

Für andere Gleichungen fünften Grades wie zum Beispiel

gibt es hingegen keine Darsellung der Lösungen mittels mehrfach geschachtelter Wurzelausdrücke. Gleiches gilt für die meisten anderen Gleichungen, die man erhält, wenn man die Koeffizienten der Gleichung vom Grad 5 einfach zufällig, beispielsweise aus dem Bereich der ganzen Zahlen, auswählt. Wie aber kann man einer fünften Grades Gleichung "ansehen", ob sie mittels eines verschachtelten Wurzelausdruckes auflösbar ist oder nicht?

Unter Hinweis auf die auf Evariste Galois zurückgehende Galois-Theorie dürften die meisten Mathematiker diese Frage etwa wie folgt beantworten:

Jeder solchen Gleichung ist eine so genannte Gruppe, die so genannte Galois-Gruppe, zugordnet, wobei es sich um ein abstrakt definiertes, aber auf jeden Fall endliches Objekt handelt. Diesem Objekt kann man dann relativ einfach ansehen, ob die ursprüngliche Gleichung auflösbar ist oder nicht.

Beispielsweise besitzt die Galois-Gruppe der erstgenannten Gleichung 10 Elemente, während die zweitgenannte Gleichung zu einer Galois-Gruppe mit 120 Elementen führt.

Auch wenn damit die "größere Komplexität" der zweiten Gleichung immerhin theoretisch "greifbar" wird, stellt sich natürlich die Frage, ob diese erhöhte Komplexität auch irgendwie elementar, etwa auf Basis irgendeiner Formel ersichtlich ist. Dies ist in der Tat der Fall.

Aber schauen wir uns zunächst an, in welcher Hinsicht sich die beiden Gleichungen nicht unterscheiden:

Beide Gleichungen besitzen jeweils 5 Lösungen. Dies gilt übrigens auch für jede andere Gleichung fünften Grades, wobei bei anderen Gleichungen fünften Grades durchaus auch ein Teil dieser fünf Lösungen zusammenfallen kann.

Generell hat, wie es erstmals von Carl Friedrich Gauß bewiesen wurde, jede Gleichung n-ten Grades stets n (nicht zwangsläufig verschiedene) Lösungen im Bereich der komplexen Zahlen. Das heißt, jedes Polynom n-ten Grades besitzt eine Produktzerlegung der Form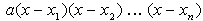

Die linke Seite beider Gleichungen lässt sich nicht in das Produkt von zwei Polynomen niedrigerer Grade mit rationalen Koeffizienten, etwa in das Produkt eines quadratischen und eines kubischen Polynomes, zerlegen. Beide Polynome fünften Grades sind also irredzibel (unzerlegbar) über den rationalen Zahlen, wie man diese Eigenschaft nennt.

Worin besteht aber nun der Unterschied? Welche elementar formulierbare algebraische Eigenschaft bewirkt, dass die erste Gleichung mittels eines verschachtelten Wurzelausdruckes auflösbar ist und die zweite nicht? Die Antwort ist einfacher, als vielleicht selbst einige mit der Galois-Theorie flüchtig in Berührung gekommene Mathematiker vermuten würden: Für die erste Gleichung lässt sich (bei geeigneter Nummerierung der Lösungen) die Identität

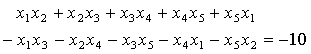
Relation zwischen den Wurzeln

finden. Für die zweite Gleichung existiert, egal wie man die Lösungen auch nummeriert, keine solche Identität, das heißt, der gerade angeführte Ausdruck in den fünf Lösungen x₁, ..., x₅ nimmt nie einen rationalen Wert an.

So "elemenatar" und intuitiv diese Sichtweise auflösbarer Gleichungen auf den ersten Blick erscheinen mag: Strukturelle Einsichten, wie kompliziert eine aufzulösende Gleichung ist, vermittelt richtig erst die Galois-Gruppe einer Gleichung. Ihrer Definition liegt die Idee zugrunde, Identitäten zwischen den Lösungen auf ihre wesentliche Substanz dadurch zu reduzieren, dass diejenigen Symmetrien der Lösungsmenge bestimmmt werden, welche die zu einer Gleichung gehörenden Identitäten respektieren. Für die angeführte Gleichung sind dies genau 10 Permutationen (Vertauschungen) der fünf Lösungen.

Abseits des allgemeinen mathematischen Hintergrundes kann man natürlich auch danach fragen, wie man für eine konkret vorliegende Gleichung fünften Grades solche Identitäten zwischen den Lösungen findet beziehungsweise ausschließt: Dazu lässt sich mittels allgemeiner Formeln aus den Koeffizienten der Gleichung eine so genannte Resolventen-Gleichung sechsten Grades berechnen. Eine irreduzible Gleichung fünften Grades mit rationalen Koeffizienten ist nämlich genau dann mit Radikalen (geschachtelten Wurzelausdrücken) lösbar, wenn diese Resolventen-Gleichung sechsten Grades eine rationale Lösung besitzt. Dieses Kriterium ist im konkreten Fall immer mit überschaubarem Aufwand prüfbar. Details werden in Kapitel 8 meines Buches Algebra für Einsteiger: Von der Gleichungsauflösug zur Galois-Theorie beschrieben.

Jörg Bewersdorff